1. Maximum flow problem
    1. Definition
    2. Transformation
    3. Residual Network
      1. Augmenting Paths
    4. The Ford Fulkerson Method
    5. Reference

This problem involves solving the equivalent maximum flow problem. We can use Ford–Fulkerson algorithm with BFS to calculate the total flow.

Maximum flow problem

We can use a directed graph as a flow network where the source produces the elements at some rate and the sink consumes the material at the same rate.

Definition

We define a flow network $G = (V, E)$ as a directed graph in which each edge $(u, y) \in E$ has a nonnegative capacity $c(u, v) \ge 0$ and there is not an edge $(v, u)$ in the reverse direction. We distinguish two vertices in a flow network: a source s and a sink t, thus for each vertex $v \in V$, the flow network contains a path $ s \rightsquigarrow v \rightsquigarrow t$. A flow in $G$ is a real-valued function $f: V \times V \to R$ that satisfies $0 \le f(u, v) \le c(u, v)$ and flow conservation implies for all $u \in V - \\\\{s, t\\\\}$, $\sum_{v \in V} f(v, u) = \sum_{v \in V} f(u, v)$.

We call the nonegative quantity $f(u, v)$ the flow from vertex $u$ to vertex $v$. When $(u, v) \notin E$, there can be no flow from $u$ to $v$, and $f(u, v) = 0$. The value $|f|$ of a flow $f$ is defined as $|f| = \sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s)$. In the maximum-flow problem, we are given a flow network $G$ with source $s$ and sink $t$, and we wish to find a flow of maximum value.

Transformation

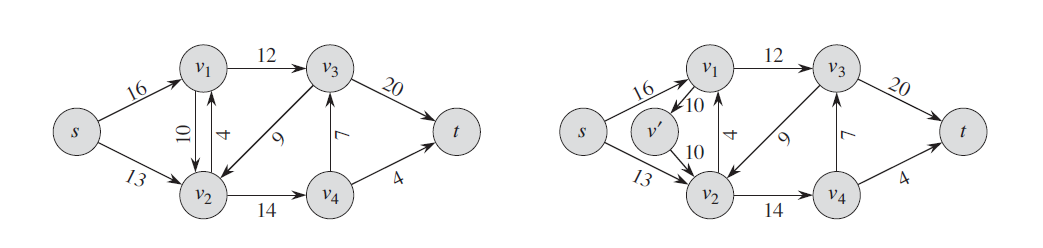
We call the two edges $(v_1, v_2)$ and $(v_2, v_1)$ antiparallel. And if we wish model a flow problem with antiparallel edges, we must transform the network into an equivalent one containing without antiparallel edges by adding a new vertex $v^\prime$ and replacing edege $(v_1, v_2)$ with the pair of edges $(v_1, v^\prime)$ and $(v^\prime, v_2)$.

Equivalent Antiparallel Flow

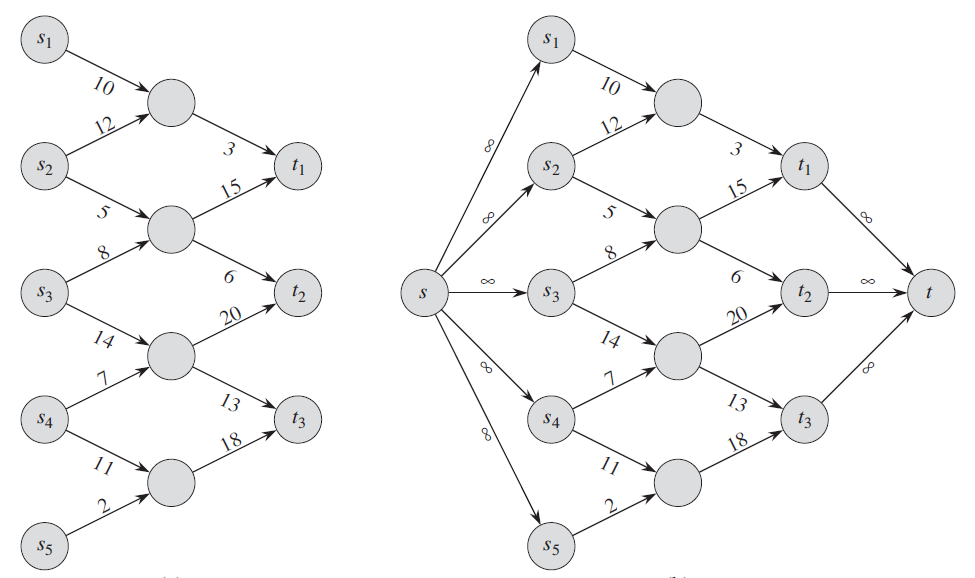
When there are several sources and sinks, we can reduce the problem to an ordinary maximum flow problem by adding a supersource $s$ and a directed edge $(s, s_i)$ with capacity $c(s, s_i) = \infty$ for each $i=1, 2, …, n$ and a new supersink $t$ and a directed edge $(t_i, t)$ with capacity $c(t_i, t) = \infty$ for each $i = 1, 2, .., n$.

Equivalent Multiple Sources Sinks Flow

Residual Network

Given a flow network $G = (V, E)$ with source $s$ and sink $t$ and a flow $f$, the residual network $G_{f}$ consists of residual edges with capacities $c_{f}(u, v)$

$$
c_{f}(u, v) =
\begin{cases}
c(u, v) - f(u, v) & \text{ if } (u, v) \in E\\\\
f(v, u) & \text{ if } (v, u) \in E\\\\
0 & \text{otherwise}\\\\
\end{cases}
$$

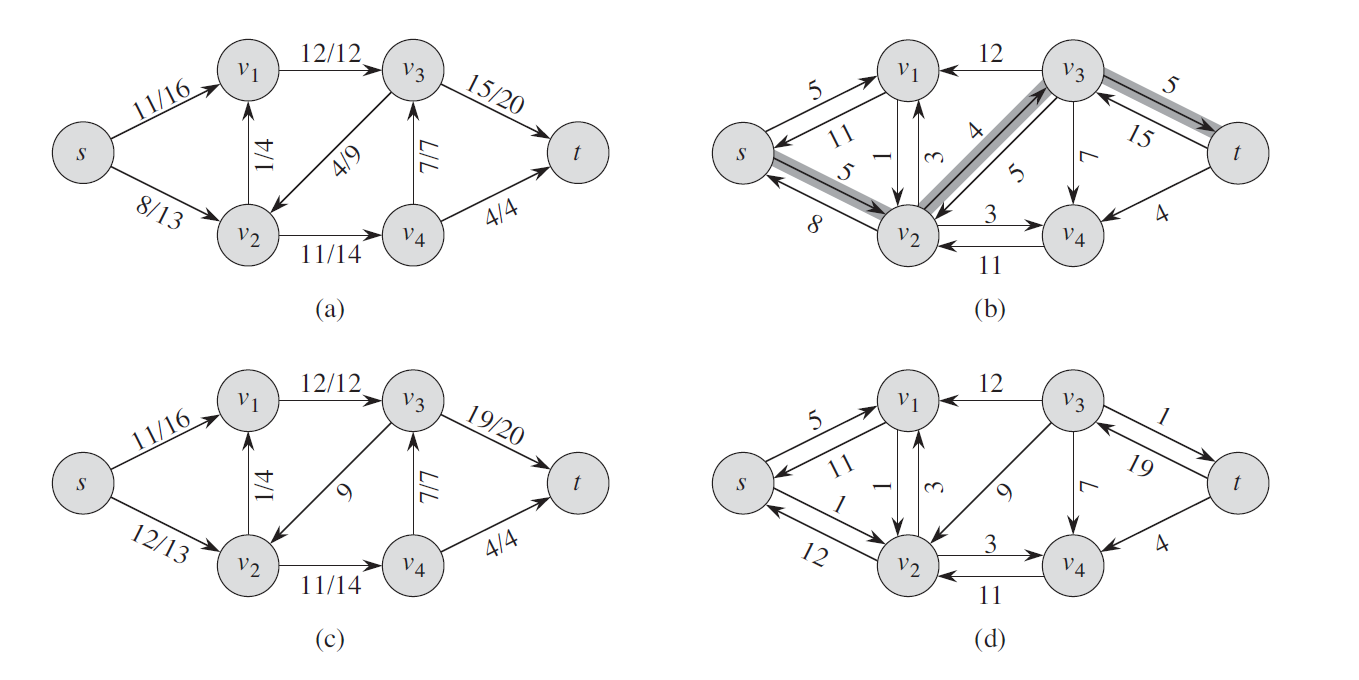
Residual Network

Augmenting Paths

Given a flow network $G = (V, E)$ and a flow $f$, an augmenting path $p$ is a simple path from $s$ to $t$ in the residual network $G_{f}$. We call the maximum amount by which we can increase the flow on each edge in an augmenting path $p$ the residual capacity of $p$, given by $c_f(p) = \min{ \\\\{ c_f(u, v) : (u, v) \text{ is on } p \\\\} }$.

The Ford Fulkerson Method

The Ford-Fulkerson method is a greedy algorithm that iteratively increases the value of the flow. At each iteration.

Given a network $G = (V, E)$ with flow capacity $c$, a source node $s$ and a sink node $t$

  1. $f \leftarrow 0$
  2. $f(u, v) \leftarrow 0$ for all edges $(u, v) \in E$
  3. while there exists an augmenting path $p$
    1. Find $c_f(p)$
    2. $f \leftarrow f + c_f(p)$
    3. for each edge $(u, v) \in p$
      1. if $(u, v) \in E$
        1. $f(u, v) \leftarrow f(u, v) + c_f(p)$
      2. else
        1. $f(v, u) \leftarrow f(v, u) - c_f(p)$
  4. return $f$

Escape Pods

Reference